介绍线概率一些知识。概率论是表示不确定的数学基础。它提供了表示表示不确定的方法和求解不确定表达式的公理。在人工智能领域，概率论主要有两种用途。1、概率论告诉我们人工智能怎么推论，因此我们可以设计算法计算或近似由概率论推导出来的公式。2、可以使用概率论和统计在理论上分提出的AI系统的行为。

概率论是许多科学和工程的基础工具。这一节确保一些数学不扎实的软件工程师可以理解本书的数学。

3.1 为什么需要概率？

计算机科学的许多分支处理的实体都是确定的。程序员可以安全的假设CPU将会完美无瑕地执行机器指令。硬件引起的问题太少了，以至于许多软件应用在设计时不用考虑它的发生。对比许多计算机工程师在相对稳定确定的环境下工作，机器学习使用概率论可能会让人惊讶。

机器学习处理的的事情是不确定的，有时还需要处理随机（非不确定）事情。而不确定性和随机性来自许多方面。总结一下，大概来自三个方面：
1、系统模型固有的随机性：例如，大部分量子论的解释，把原子内的微粒当做不确定的。例如洗牌，理论上我们假设了牌真正的随机洗过了。
2、不完整的观察：即使系统是确定的，但是我们也不能观察到所有影响系统行为的变量。
3、不完整的建模：当我们建模是，要舍弃一些信息。舍弃的信息导致模型预测的不确定性。

在许多实践中，更倾向于使用简单不确定的规则，也不去使用确定复杂的规则。例如，“鸟会飞，设计起来很简答”；但是真正正确的表述应该是“鸟当中，除了没有学会飞的幼鸟、生病的鸟、受伤的失去飞翔能力的鸟……，才会飞”。

概率论原本是描述事情发生的频率的。例如，在抽扑克游戏中，我们说一定概率$p$抽到某张牌，那么抽很多次，会大概有$p$比例的次数抽到这张牌；这是可以重复的实验。有些是不能重复的，例如一个医生说病人有40%的可能性患有流感，我们不能重复多次得到病人的拷贝来验证。这时需要信度degree of belief，1代表病人确定患有流感，0代表病人一定没有流感。
在上面两个例子中，第一种事件以一定概率发生，叫做频率概率frequentist probability。后一种，定性的准确性（例如诊断为流感情况下，诊断准确性的概率）叫做贝叶斯概率Bayesian probability。

如果要列出关于不确定性共有的特性，那么就是把贝叶斯概率和频率概率当做一样。例如，选手手中的牌已知，计算他赢得扑克游戏的概率；这和病人有某种症状，他患有某种病的概率计算方法相同。

概率论可以看做逻辑处理不确定性的拓展。在确定了命题A的真伪后，逻辑学为我们推导基于命题A的情况下，命题B的真伪；而概率论命题B真或伪可能性的大小。

3.2随机变量

随机变量是可以随机取一些值的变量。经常在变量右下角加上数字下标来表示随机变量可能的取值。例如，$x_1,x_2$是随机变量x可能取的值。如果是向量的话，x是随机变量，$x$是它可能取得值。

随机变量可能连续，可以能离散。离散随机变量状态有有限种，这些状态可以和数字无关。连续随机变量和一个实数相关联。

3.3 概率分布

概率分布是用来描述变量怎么分布在各个状态的。描述变量分布的方式要取决于这个变量是离散，还是连续。

3.3.1 离散变量和概率质量函数

离散变量的概率分布用概率密度函数（probability mass function, PDF），经常用$P$表示。

概率质量函数把一个状态映射为这个状态出现的概率。例如$\textrm{x}=x$用$P(x)$表示；如果其值为1，表示一定是等于$x$，如果值为零，表示一定不等于$x$。$P(x)$可以这样写$P(\textrm x = x)$，或者$\textrm x \sim P(\textrm x)$

如果有多个变量，其联合分布$P(\textrm x = x, \textrm y = y)$表示$\textrm x = x, \textrm y = y$的概率，也常常简写为$P(x,y)$。

关于离散随机变量$x$的概率质量函数$P$满足一下性质：
1、$P$要覆盖$x$可能取值的所有状态。
2、$\forall x \in \textrm x, 0 \leq P(x) \leq 1$
3、$\sum_{x \in \textrm x} P(x) = 1$

3.3.2 连续变量和概率密度函数

连续变量的分布使用概率密度函数（Probability density function, PDF）来$p$表示，它满足
1、$p$必须覆盖变量$x$状态的所有范围
2、$\forall x \in \textrm x, 0 \leq p(x)$，注意并不要求$p(x) \leq 1$
3、$\int p(x)dx = 1$

概率密度函数并没有给出这个状态出现的概率，它乘以一个区间表示状态在这个区间的概率$p(x) \delta x$
例如在区间$[a, b]$的概率$\int_{[a,b]} p(x)dx$。

假设$x$在区间$[a,b]$上服从均匀分布，用函数$u(x;a,b)$表示。对于$x \notin [a,b]$，$u(x;a,b)=0$；对于$x \in [a,b]$,$u(x;a,b)=\frac{1}{b-a}$。这样的均匀分布，还可以用$x \sim U(a,b)$表示。

3.4边际概率

我们知道关于变量集合的概率分布，有时我们还想知道在这个变量集合子集合上的概率分布。这样的概率分布叫做边际概率分布（Marginal Probability）。

离散变量时，$P(\textrm x, \textrm y)$，可以使用求和准则得到
$$ \forall x \in \textrm x, P(\textrm x = x) = \sum_y P(\textrm x = x, \textrm y = y) $$
可以把$P(\textrm x, \textrm y)$写成行和列的形式，那么求一行的和（或一列的和）就可以求得上式。

对于连续变量，使用积分代替求和
$$ p(x) = \int p(x,y)dy $$

3.5 条件概率

条件概率是在某事件已经发生情况下，另一个事件发生的概率。例如$\textrm x = x$已经发生时，$\textrm y = y$的概率为
$$ P(\textrm y = y| \textrm x = x) = \frac{P(\textrm y =y, \textrm x = x)}{P(\textrm x = x)} $$
注意，上式中$P(\textrm x = x) > 0$

3.6 条件概率的链式法则

联合概率函数，可以分解为只有一个变量的概率分布函数
$$ P(\textrm x^{(1)},\dots, \textrm x^{(n)}) = P(\textrm x^{(1)}) \prod_{i=2}^n P(\textrm x^{(i)}|\textrm x^{(1)},\dots,x^{(i-1)}) $$
可能看起来不太直观，直观一点为：
$$ P(\textrm x^{(1)},\dots, \textrm x^{(n)})=P(\textrm x^{(1)}) P(\textrm x^{(2)}|\textrm x^{(1)}) P(\textrm x^{(3)}|\textrm x^{(1)} \textrm x^{(2)}) \dots $$
这是条件概率的链式法则。将上面定义应用两次
$$ P(a,b,c) = P(a|b,c) P(b,c) $$
$$ P(b,c) = P(b|c) P(c) $$

$$ P(a,b,c)= P(a|b,c) P(b|c) P(c) $$

3.7独立和条件独立

如果两个变量独立，那么它们的联合概率等于它们概率的乘积。即$x,y$独立
$$ \forall x \in \textrm x, y \in \textrm y, p(\textrm x = x, \textrm y = y)=p(\textrm x = x)p(\textrm y = y) $$
可以用$\textrm x \perp \textrm y$表示。

$x,y$在给定$z$是条件独立
$$ \forall x \in \textrm x, y \in \textrm y, z \in textrm z, p(\textrm x = x, \textrm y = y|\textrm z = z)=p(\textrm x = x|\textrm z = z)p(\textrm y = y|\textrm z = z) $$
可以用$\textrm x \perp \textrm y|\textrm z$表示。

3.8 期望，方差和协方差

函数$f(x)$关于概率分布$P(\textrm x)$的期望可以用求和或积分求得：
$$ E_{x \sim P}[f(x)]=\sum_x P(x)f(x) $$
或
$$ E_{x \sim P}[f(x)]=\int P(x)f(x)dx $$

期望是线性运算，例如
$$ E_x[\alpha f(x) + \beta g(x)] = \alpha E_x[f(x)] + \beta E_x [g(x)] $$
其中$\alpha, \beta$不依赖$x$

方差用来描述变量的波动大小的，定义如下：
$$ Var(f(x)) = E[(f(x) - E[f(x)])^2] $$
如果方差比较小，说明$f(x)$聚集在其期望附近。方差的平方根叫做标准差。

协方差用来描述两个变量的线性依赖关系的强弱，定义如下
$$ Cov(f(x),g(x)) = E[(f(x)-E[f(x)])(g(y)-E[g(y)])] $$
如果协方差绝对值比较大，说明两个变量同时距离均值比较远。如果取值为正，说明两者同时变大；如果为负，说明两者一个变大，另外一个变小。其他衡量方法，例如相关系数，是把分布标准化，用来衡量它们之间相关性的大小。

协方相关和依赖有关系，但是它们是不同的概念。有关系，是因为两个独立的变量的方差为零；如果两个变量的协方差不为零，那么它们有依赖。独立和协相关是两个不同的属性。如果两个变量协方差为零，那么它们一定没有线性依赖关系。独立的要求更高，因为独立不仅仅要求非线性相关；零协方差只表示非线性相关。

例如从在区间$[-1,1]$上均匀分布上去一点$x$，在集合$(-1,1)$中取一个数$s$。假设$y=sx$，$s$决定符号，而$x$决定幅度。显然$x,y$相关，但是$Cov(x,y)=0$。

向量$x \in R^n$的协方差矩阵是一个$n \times n$的矩阵
$$ Cov(\mathbf x)_{i,j} = Cov(x_i,x_j) $$
协方差矩阵的对角就是方差
$$ Con(x_i,x_i)=Var(x_i) $$

3.9常用概率分布

介绍几个常见的概率分布

伯努利分布

伯努利分布式一个二项分布，它只有一个变量表示等于1的概率：$\phi \in [0,1]$
$$P(\textrm x = 1) = \phi$$
$$P(\textrm x = 0) = 1-\phi$$
综合一下为：
$$P(\textrm x = x) = \phi^x(1-\phi)^{1-x} $$
期望和方差为：
$$E_{\textrm x}[\textrm x] = \phi$$ $$Var_{\textrm x}(\textrm x) = \phi(1-\phi)$$

多项分布

伯努利分布只有2个状态，多项分布状态可以大于2个。
伯努利分布和二项分布在离散变量分布中常常用到，因为离散变量状态可以统计。连续变量状态时，上面两个分布就不适用了。

高斯分布

高斯分布也叫作标准分布：
$$ \mathcal N(x;\mu, \sigma^2)=\sqrt{\frac{1}{2 \pi \sigma^2}}\exp(-\frac{1}{2\sigma^2}(x-\mu)^2) $$
分布有两个参数$\mu \in R$和$\sigma \in (0, \infty)$控制，前者是均值，后者是方差:$E(x)=\mu, Var(x)=\sigma^2$.

还有一种形式
$$ \mathcal N(x;\mu, \beta)=\sqrt{\frac{\beta}{2 \pi}}\exp(-\frac{1}{2}\beta(x-\mu)^2) $$
在应用中常常使用高斯分布。在缺少先验知识情况下，使用高斯分布是一个明智的选择。因为：
1、我们要估计的分布可能就接近高斯分布。
2、在方差大小相同情况下，高斯分布包含的不确定性最大（即信息量最大）。

上面是单变量的高斯分布，把它扩展到多维叫做多方差标准分布，要用到正定对称矩阵$\Sigma$
$$ \mathcal N(x;\mu, \Sigma)=\sqrt{\frac{1}{(2 \pi)^n det(\Sigma)}}\exp(-\frac{1}{2}(x-\mu)^T \Sigma^{-1}(x-\mu)) $$
$\mu$是分布的均值，这时是个矩阵。$\Sigma$是分布的协方差矩阵。还可以写成
$$ \mathcal N(x;\mu, \beta^{-1})=\sqrt{\frac{det(\beta)}{(2 \pi)^n }}\exp(-\frac{1}{2}(x-\mu)^T \beta(x-\mu)) $$
经常把协方差矩阵变为对角矩阵。还有一个更简单的isotropic高斯分布，它的协方差矩阵为单位矩阵乘以一个标量。

指数和拉普拉斯分布

在深度学习中，我们经常想要一个在$x=0$处有尖点（sharp point）的概率分布，指数分布（exponential distribution）就能满足这一点
$$ p(x; \lambda)=\lambda \textbf 1_{x \geq 0} \exp(-\lambda x) $$
其中$1_{x \geq 0}$表示当$x$为负数时，概率为零。

一个近似相关的拉普拉斯分布（Laplace distribution）可以让我们在点$\mu$有锐点
$$ \text{Laplace}(x;\mu,\gamma)=\frac{1}{2\gamma} \exp (-\frac{|x-\mu|}{\gamma}) $$

狄拉克分布和经验分布

在一些实例中，我们希望把概率分布的的所有质量（mass）都聚集到一个点，这时可以使用狄拉克分布$\delta(x)$
$$ p(x)=\delta(x-\mu) $$
$\delta(x)$在非零点，其值为0，但是它积分还是1。狄拉克分布不是普通的函数，它是泛化函数（generalized function）。可以这样认为：狄拉克函数把其他地方所有的质量都一点点集中到了0处。它在$x=0$时值无限大，因为积分为1。

还有一个更常用的有狄拉克组成的分布，叫做经验分布
$$ \hat p(x)=\frac{1}{m}\sum_{i=1}^{m}\delta(x-x^{(i)}) $$
狄拉克分布是定义在连续变量上的。

我们可以把狄拉克分布看做，从训练集中采样一些样本，使用采样的样本训练训练模型。

混合分布

常常联合几个概率分布来定义新的概率分布。经验分布就是狄拉克分布组合而来。

在使用联合混合分布时，那个分布起作用可以用多项分布控制
$$ P(x) = \sum_i P(c = i)P(x|c=i) $$
其中$P(c)$就是一个多项分布。

混合模型中，可以引出一个概念：潜在变量（latent variable）。潜在变量使我们不能直接观察到的变量，在上面的混合模型中$c$就是一个例子。潜在变量通过联合概率分布和$x$产生联系$P(x,c)=P(x|c)P(c)$，分布$P(c)$并不能直接观察到，但是我们还是可以定义$P(x)$

非常重要和常用的联合模型是高斯混合模型，其中$p(x|c=i)$是高斯的。每个组成部分有单独的均值$\mu^{(i)}$和方差$\Sigma^{(i)}$；在一些混合模型中，可能有对变量有更多限制。

除了均值和方差，高斯混合分布指定了每个$i$的先验分布（prior probability）$\alpha_i = P(c=i)$。先验是指在观察到$x$以前已经知道$c$。一个对比，$P(c|x)$是后验概率，因为它在观察到$x$后才计算。高斯混合模型是常用的近似密度，因为任何平滑的密度都可以被多变量高斯混合模型近似。

3.10常用函数的有用特性

logistic sigmoid
$$ \sigma (x) = \frac{1}{1 + \exp(-x)} $$
常常用来生成伯努利分布，因为它的输出范围是$(0,1)$。

softplus
$$ \zeta(x) = log(1 + \exp(x)) $$
softpuls常常为标准分布生成$\beta$或$\sigma$，因为它的输出范围是$(0, \infty)$

softpuls使用$max(0,x)$变化而来的，是它的平滑版本。

下面性质很有用，希望你能记住
$$ \sigma(x) = \frac{\exp(x)}{\exp(x) + \exp(0)} \\\ \frac{d}{dx}= \sigma(x)(1-\sigma(x)) \\\ 1-\sigma(x) = \sigma(-x) \\\ \log(\sigma(x) = -\zeta(-x) \\\ \frac{d}{dx}\zeta(x) = \sigma(x) \\\ \forall x \in (0,1), \sigma^{-1}(x)=\log\frac{x}{1-x} \\\ \forall x > 0, \zeta^{-1}(x)=\log(\exp(x) - 1) \\\ \zeta(x)=int_{-\infty}^{x}\sigma(y)dy \\\ \zeta(x) - \zeta(-x)=x $$

3.11贝叶斯准则

已知$P(y|x)$，想知道$P(x|y)$；如果知道$P(x)$，可以使用贝叶斯准则计算
$$ P(x|y)=\frac{P(x)P(y|x)}{P(y)} $$
$P(y)$可以通过$P(y)=\sum_{x}P(y|x)P(x)$计算得来。
贝叶斯准则使用计算条件概率的。

3.12连续变量的一些技术细节

对于两个连续变量$x,y$，有如下关系$y=g(x)$，这里$g$是连续、可逆、可谓分的变换。现在来找$p_y(y)$和$px(x)$的关系。
$$ |p_y(g(x))dy|=|p_x(x)dx| $$
可以得到
$$ p_y(y)=p_x(g^{-1}(y))\frac{\partial x}{\partial y} $$ 另一种形式 {% raw %} $$ p_x(x)=p_y(g(x))\frac{\partial g(x)}{\partial x} $$
在高维空间中，微分泛化为雅克比矩阵的行列式$J{i,j}=\frac{\partial x_i}{\partial y_j}$
$$ p_x(x)p_y(g(x))|\det (\frac{\partial g(x)}{\partial x})| $$

3.13信息论

衡量一个事件的信息量，应该有一下准则：
1、发生概率越大的事件包含信息量越小。
2、发生可能性越小的事件，包含信息量越大。
3、相互独立的事件，信息量可以相加

定义自信息（self-information）,$\textrm x = x$
$$ I(x)=-\log P(x) $$
自信息只是定义单个事件，衡量一个概率分布的信息量使用香农熵（Shannon entropy）
$$ H(x) = E_{x \sim P}[I(x)] = -E_{x \sim P}[\log P(x)] $$
有两个关于$x$的分布$P(x)$、$Q(x)$，衡量两个分布的不同，可以使用相对熵（Kullback-Leibler divergence）
$$ D_{KL}(P||Q)=E_{x \sim p}[\log \frac{P(x)}{Q(x)}]=E_{x \sim p}[\log P(x) - \log Q(x)] $$
在机器学习中，常常这样使用：$P$是真实分布，从中抽取一些符号，用来估计分布得到$Q$，要做的就是最小化$D_{KL}$。

$D{KL}$有许多有用的特性，用的最多的就是非负性。它用来衡量两个分布的距离，用一个分布估计另一个分布，最小化它们之间的$D{KL}$即可。注意，$D{KL}$不是非负的。$D{KL}(P||Q) \neq D_{KL}(Q||P)$，在使用时要注意用哪个。

它和交叉熵相关，交叉熵为$H(P,Q) = H(P) + D_{KL}(P||Q)$，缺少左边部分，变为：
$$ H(P,Q) = -E_{x \sim P} \log Q(x) $$
最小化和$Q$相关的交叉熵等价于最小化KL距离，因为$Q$和$H(P)$无关，忽略它。

3.14构造概率模型

机器学习中的概率分布经常和许多变量相关。但是这些概率分布常常只和几个变量直接相关。使用单一函数构造概率分布效率低下，这时可以把概率分布划分为几个相关因子，之后再相乘。例如有三个变量$a,b,c$，$a$影响$b$，$b$影响$c$，但是在给定$b$时$a,c$不相关。可以这样描述这个分布
$$ p(a,b,c) = p(a)p(b|a)p(c|b) $$
这个因式分解可以极大减少描述分布的参数。

可以用图来描述这样的因式分解：顶点的集合通过边来互相连接。当用图来表示概率的因式分解时，叫做构造概率模型后图模型。

主要有两种类型的构造概率模型：有向模型的和无向模型。两种类型都是使用图，顶点表示一个变量，通过边相关联的两个变量表示这两个变量在概率分布中有直接关系。

有向模型：图中的边是有向。如下图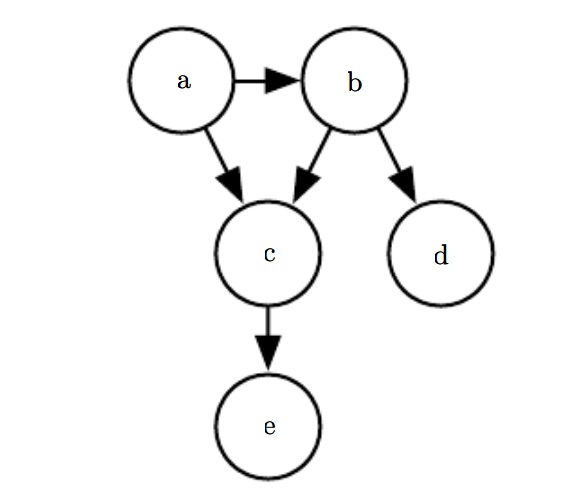

关联的顶点的概率和它的父节点变量相关，父节点定义为$Pa_{\mathcal G}(x_i)$
$$ p(x) = \prod_i p(x_i|Pa_{\mathcal G}(x_i)) $$
无向模型使用无向表示，它表示因式分解时使用一系列函数；这些函数和有向模型不同，它们不是任何形式的概率分布。几个顶点的集合叫做圈（clique），一个圈在一用变量$\phi^{(i)}(C^{(i)})$表示，它表示函数而不是分布。每个函数的输出大于0，但是并不保证其积分等于1。可以除以$Z$归一化，归一化后的概率分布为：
$$ p(x) = \frac{1}{Z}\prod_i \phi^{(i)}(C^{(i)}) $$
如下图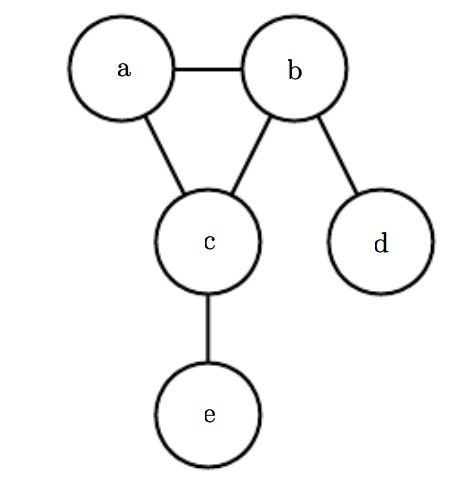

概率分布为：
$$ p(a,b,c,d,e)=\frac{1}{Z}\phi^{(1)}(a,b,c)\phi^{(2)}(b,d)\phi^{(3)}(c,e) $$